Number of Turns, Revisited.

The number of turns that i estimated on the new coils doesn't seem quite right. which it probably isn't as for the most part its was a complete guess. I thought it may be interesting to put some bounds on this number and do some estimation, so here we go.

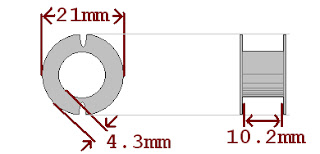
The bobbins that I'm using have a window area of about 44mm^2. This is a measure of how much area for copper the coil has. Here, its found by multiplying 4.3mm and 10.2mm. Since the wire i'm using has a diameter of 0.16mm, it has a cross sectional area of 0.02mm^2. This means that at most there could be 2200 turns on this bobbin, probably less. This would be the case if there where no air gaps in between wire, which is impossible as the wire is round. More reasonably, we could look at if the wire a lined up in a grid, each piece sitting on-top of each-other for the maximum airspace. this would give us about 1700 turns. So if i wrapped this perfectly, i would have between 1700 and 2200 turns per coil. Of course i didn't wrap this well, so it's probably much less than this.

When wrapping magnetics, people usually use a scale factor called the "fill factor", or "window utilization factor". This term approximates how much of the window area is actually filled with  copper, vs how much is filled with air due to gaps between turns. This is a percentage, where a fill factor of 0.9 means that 90% of the window area is used by copper, with the remaining 10% filled with air or insulation, etc. The fill factor can vary between about 0.05 for high voltage transformers with lots of isolation between wires, and about 0.5 for a simple hand wound inductor. Using special materials like a foil instead of wire (which rips all the time and is just horrible to work with), or square wire (which is a pain to wrap) can get this number up to about 0.65. For this coil, 0.3 is about the worst reasonable, which gives us 660 turns as a lower bound.

Putting this together, ill use 1700 as an unreasonable upper bound, and 660 as a lower bound. its a decently wide range, but lets me know that i have way more turns than i expected, which makes sense due to the much larger voltages that i was getting.

As a double check, we can measure the resistance of the wires. The inner winding radius is 6.2mm, while the outer is 10.5mm. This gives us an average of 8.35mm, which ill bump up to 9mm because if how things are wound on the bobbin. This leaves us with an average turn length (amount of wire used on each turn) of about 56mm. At room temperature, AWG34 wire has a resistance per meter of about 0.86Ohms. The coils i wound have resistances of 38.1Ohms, and 34.3Ohms, giving approximate number of turns of about 790 and 710 for the two coils. This makes sense, as one gives a slightly higher voltage spike than the other.

So that was fun.